不等式 の 表す 領域 問題

アレジア どこ の 国2講 不等式の表す領域（3節 軌跡と領域） 問題集【3章 図形と . 2講 不等式の表す領域（3節 軌跡と領域） 問題集【3章 図形と方程式】です。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお. 数学における領域と不等式 不等式の表す領域の図示 | 高校数学 . 不等式 の 表す 領域 問題問題1. 問題2. 問題3. 不等式 の 表す 領域 問題まとめ. 不等式 の 表す 領域 問題そもそも領域って何？ 図形と方程式の範囲で最後に出てくるのがこの 「領域」 の分野です。 ここで考えている「領域」というものは一体何なのかをまずは理解するところから始めましょう。 数学における領域とは. 不等式 の 表す 領域 問題ある x 、 y の不等式を満たす ( x, y) という組を全て集めた集合. 不等式 の 表す 領域 問題です。 言葉で書くと難しそうに聞こえるのですが、簡単な例でこの意味を確認してみたいと思います。 例えばこんな不等式があったとしましょう。 y > x + 3. この不等式を満たす ( x, y) という組は 無数にあります。 例えば ( 1, 5) とか ( 4, 20) とか。 いっぱいありますよね。. 【高校数学Ⅱ】「不等式の表す領域（1）」(例題編) | 映像授業 . 解説. 不等式 の 表す 領域 問題これでわかる! 例題の解説授業. 不等式が表す領域を図示する問題ですね。 ポイントは以下の通りでした。 POINT. 不等式 の 表す 領域 問題境界線の上側か下側かを見極めよう. 境界線は y=x+1 となりますね。 不等号の向きは ＞ なので、表す領域は 境界線の上側 になりますね。 ここで注意! 式を見ると不等号に ＝はついていません ね。 この 領域は境界線を含まない といえます。 「境界線を含まない」という言葉を必ず書きましょう。 (1)の答え. 境界線は y=-2x+3 です。 不等号は ≦ なので、領域は境界線の下側とわかります。 式は＝を含んでいるので、 境界線は含みます ね! (2)の答え. 不等式の表す領域（1） 146.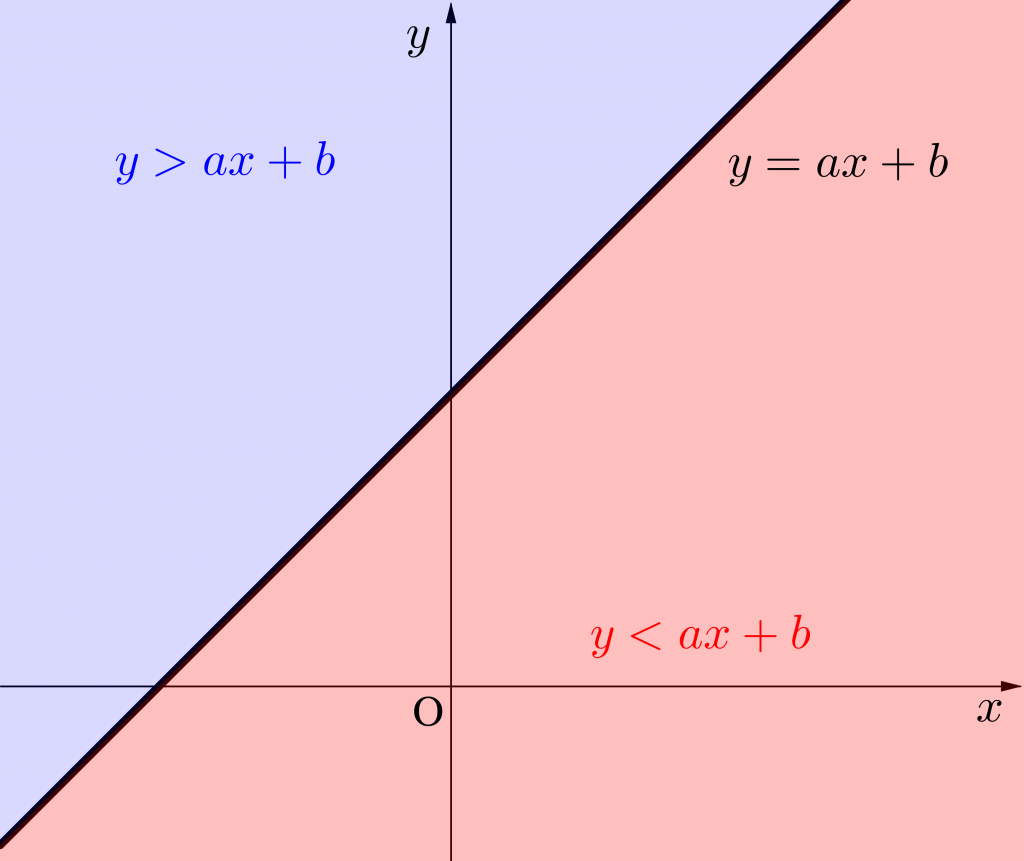

友達にシェアしよう! 軌跡と領域の例題. 不等式 の 表す 領域 問題不等式の表す領域（2）. 数学Ⅱ｜不等式の表す領域の求め方とコツ | 教科書より詳しい . 今回の問題は「 不等式の表す領域 」です。. 問題 次の不等式の表す領域を求めよ。. (1) y ≦ −2x + 3. (2) x < 3. (3) y ≦ −1. (4) x2 +y2 ≧ 5. (5) y < −x2 + 2x. 次のページ「解法のPointと問題解説」. 【高校数学Ⅱ】不等式の表す領域（基本） | 受験の月. 不等式の表す領域（基本） AB>0、AB<0型の不等式の表す領域 絶対値付き不等式 |x+y|≦a、|x|+|y|≦a の表す領域 正領域と負領域、直線と線分が交わる条件 放物線と線分が交わる条件 三角形の内接円の方程式 2変数不等式の命題と. 【高校数学の分かりやすいサイト】問題解説「不等式の表す領域」. 17 歳 の カルテ リサ 病名

赤城 ちゃん の おいしい おしっこ かけ ご飯今日は不等式の表す領域の問題だよ。 図をかきながら考えよう。 目次. 問題. 解答. 問題1の解答. 不等式 の 表す 領域 問題問題2の解答. 問題3の解答. 問題1. 3点 A(−1,2), B(4,1), C (1,5) A ( − 1, 2), B ( 4, 1), C ( 1, 5) を頂点とする ABC A B C の内部および周を表す不等式を求めよ。 問題2. 点 (x,y) ( x, y) が問題1の ABC A B C の内部及び周上を動くとき， 2x + y 2 x + y. の最大値と最小値を求めよ。 問題3. 点 (x,y) ( x, y) が問題1の ABC A B C の内部及び周上を動くとき， x2 + y2 x 2 + y 2. の最大値と最小値を求めよ。 解答. 不等式の表す領域：領域での最大値と最小値、図形の通過領域 . 1 方程式によって異なる不等式の表す領域 1.1 連立方程式による不等式の表す領域 1.2 絶対値を含む場合の不等式の表す領域 1.3 かけ算を含む場合、不等式の表す領域はどうなるのか 2 一次式での領域の最大値と最小値. 不等式と領域の図示 - 高校数学.net. 問題 解答. 次の不等式の表す領域を図示せよ。 (1) (2x−y+1)(x+y−2) <0 ( 2 x − y + 1) ( x + y − 2) < 0. (2) {x−2y ≧1 (x−1)2+(y+1)2 ≦4 { x − 2 y ≧ 1 ( x − 1) 2 + ( y + 1) 2 ≦ 4. (3) |x|+|y|≦ 1 | x | + | y | ≦ 1. 不等式 の 表す 領域 問題(1) (i) {2x−y+1 <0 x+y−2 >0 { 2 x − y + 1 < 0 x + y − 2 > 0. ⇔ {y >2x+1 y >−x+2 ⇔ { y > 2 x + 1 y > − x + 2. 【高校数学ⅱ】Ab>0、Ab<0型の不等式の表す領域 . 不等式 の 表す 領域 問題高校数学総覧. 高校数学Ⅱ 図形と方程式（軌跡と領域） AB>0、AB<0型の不等式の表す領域. 2020.10.23. 不等式 の 表す 領域 問題検索用コード. 円と直線の交点が (2, 0), (0, 2)であることはすぐにわかる. 求める領域は, 「 (円の外側)かつ (直線の下側)」または「 (円の内側)かつ (直線の上側)」}である. このAB>0, AB<0型の領域は, 以下のような観点でとらえると楽に図示できる. 領域の境界線となるのは, A=0とB=0を満たす曲線 (直線含む)}である. 座標平面は, この境界線によって複数の領域に分割される. 境界線A=0を越えて隣の領域に移動するとしよう. つまり, 「図形的に境界線を越える」ことは「数式的には符号の逆転」を意味する.}. 1次不等式の領域を図示する問題 / 数学II by ふぇるまー |マナペ . 不等式の領域を図示する問題. 次の不等式の表す領域を図示しなさい. キン肉 マン 銀 の マスク

小さな 恋 の 歌 音域(1) 2x＋y−1＞0. max airline へ ようこそ

唇 の 皮 を むく 癖 子供(2) 2x＋y−1＜0. (3) x≧1. (1) 2x＋y−1＞0. "2x＋y−1＞0"を変形すると"y＞−2x＋1"なので、まずはy＝−2x＋1の直線をかきます。 そして"y ＞ −2x＋1"は、yの値が"y＝−2x＋1"の直線よりも大きい点の集合ということなので、図示すると次のようになります。 "y ＞ −2x＋1"なので境界線は含みません。 (1) 2x＋y−1＜0. "2x＋y−1＜0"を変形すると"y＜−2x＋1"なので、まずはy＝−2x＋1の直線をかきます。. 2次不等式の表す領域を図示する問題[放物線ver.] - マナペディア. 不等式の表す領域 [放物線] 1次不等式の領域 や 連立不等式の表す領域 を図示する問題はすでにみてきました。. 不等式 の 表す 領域 問題ここでは、放物線を境界線とする領域を図示する問題についてみていきましょう。. 次の連立不等式の表す領域を図示してみましょう。. 不等式 の 表す 領域 問題(1) y＞x² . 【高校数学Ⅱ】「不等式の表す領域（2）」(例題編) | 映像授業 . 不等式 の 表す 領域 問題解説. これでわかる! 例題の解説授業. 円が表す領域についての問題ですね。 注目するのは 不等号の向き です。 POINT. ①円の外側にある. (x-a) 2 + (y-b) 2 ＞r 2. 左辺は半径の2乗より大きかったですね。 ②円の内側にある. 不等式 の 表す 領域 問題(x-a) 2 + (y-b) 2 ＜r 2 と式はなる。 左辺は半径の2乗より小さかったですね。 左辺は半径r 2 以上の領域. 不等式 の 表す 領域 問題円の式を座標平面上に表すため、式を整理しましょう。 x 2 +y 2 -4x≧0. 不等式 の 表す 領域 問題⇔ (x-2) 2 +y 2 ≧2 2. 境界線は、中心 (2,0)、半径2の円 になりますね。 式を見ると 左辺は半径の2乗より大きい ので、表す領域は 円の外側 になりますね。. 【高校数学Ⅱ】三角不等式の表す領域 | 受験の月. 高校数学総覧.

高校数学Ⅱ 三角関数. 三角不等式の表す領域. 不等式 の 表す 領域 問題2020.08.04. 不等式 の 表す 領域 問題検索用コード. 不等式 cos (x-y)≦12 (0≦ x≦π, 0≦ y≦π) の表す領域を図示せよ三角不等式の表す領域 求める領域は, 上図の斜線部分. 境界線を含む.} 普通に三角不等式を解いてx, yのみの不等式に変換}すれば, 後は単なる領域図示の問題である. 2変数があることは気にせず, cosθ≦12 と考えて解けばよい. 【高校数学Ⅱ】「不等式の表す領域（1）」(練習編) | 映像授業 . 不等式が表す領域を図示する問題ですね。 ポイントは以下の通りでした。 POINT. 式が2つあるときは共通部分を考えよう. この問題は式が2つありますね。 ①の領域、②の領域をそれぞれ表し、 2つの領域の共通部分 を考えていきましょう。 ①の領域はy=2/3x+2の下側. 不等式 の 表す 領域 問題まず①2x-3y+6≧0の領域を求めましょう。 2x-3y+6≧0. 不等式 の 表す 領域 問題⇔y≦2/3x+2. 境界線は y=2/3x+2 となり、不等号は ≦ なので、領域は 境界線の下側 とわかります。 式は＝を含んでいるので、 境界線は含みます ね! ②の領域はx=-2の右側. 次に②x≧-2の領域を求めましょう。 境界線は x=-2 となり、不等号は ≧ なので、領域は境界線の右側とわかります。. 不等式"(x＋y)(x−y−1)＞0"の表す領域を示す問題 - マナペディア. 不等式 の 表す 領域 問題不等式の表す領域を図示する. 次の不等式の表す領域を図示してみましょう。 (x＋y) (x−y−1)＞0. これまでみてきた問題とはちょっと異なりますね。 このタイプの不等式は、解き方が決まっていますので、しっかりとその解法をおさえておけば問題ありません。 ポイント. " (x＋y) (x−y−1)＞0"が成り立つためには. " (x＋y)＞0"かつ" (x−y−1)＞0 " または. " (x＋y)＜0"かつ" (x−y−1)＜0 " である必要があります。 "＋"と"＋"をかけたら"＋"、"−"と"−"をかけたら"＋"になる、という計算ですね。 つまり" (x＋y) (x−y−1)＞0"の表す領域は、次の2組の連立不等式. 不等式 の 表す 領域 問題<連立不等式1> ・ (x＋y)＞0. ・ (x−y−1)＞0. 数学Ⅱ｜不等式の表す領域の求め方とコツ | ページ 2 | 教科書 . 不等式の表す領域の解法. ≧ や ≦ のときは、 直線 y = mx + n 上の境界線を含みます。. 不等式 の 表す 領域 問題( ⅰ ) x > a は 直線 m の右側 となります。. 不等式 の 表す 領域 問題( ⅱ ) x < a は 直線 m の左側 となります。. ≧ や ≦ のときは、 直線 x = a 上の境界線を含みます。. ( ⅰ ) y > b は 直線 n の右側 と . 土浦 ど てき ん

英 作文 の トレーニング 無料【基本】連立不等式と領域 | なかけんの数学ノート. それぞれの不等式の表す領域は、1つ目が直線の下側、2つ目が放物線の上側であることがわかります。 直線と放物線との交点は. x 2 = x + 2 x 2 − x − 2 = 0 ( x − 2) ( x + 1) = 0 x = 2, − 1 から、 ( 2, 4), ( − 1, 1) となります。 以上から、求める領域は次のようになります。 ただ、ここで注意しないといけないのは、 境界線の点の扱い です。 例題1はどちらの式にも等号が入っていたので、境界線上の点はすべて含まれました。 しかし、この例題2は、片方は含まず、もう片方は含む、となっています。 そのため、直線上の点は含まず、放物線上の点は含む、となります。 では、交点はどうでしょうか。. 不等式 の 表す 領域 問題【高校数学Ⅱ】「不等式の表す領域（1）」 | 映像授業のTry IT . 不等式の表す領域 (1) これでわかる! ポイントの解説授業. 今回のテーマは「不等式の表す領域」です。 「領域」 とは、 x,yの不等式を満たす点 (x,y)の集合 のことを言います。 といっても、言葉だけではイメージがつきませんよね。 ポイントで確認しましょう。 POINT. 不等式 の 表す 領域 問題不等号の向きで上か下かを判断しよう! 直線l：y=mx+nがあるとき、 y＞ mx+n…①. y＜ mx+n…②. ①、②が表す領域を考えてみましょう。 ① y＞ mx+nのときには、領域は「直線の上側」になります。 ② y＜ mx+nのときには、領域は「直線の下側」になります。 POINT. そしてこの時、直線lを 境界線 といいます。 このように 不等号の向きで式の表す領域が上側か下側かを見分けます。. 対数不等式の応用問題（領域を表す例題と解説） - 効率学習 . 対数不等式の応用問題として表す領域の図示があります。 対数関数における定義と定理がポイントになりますので、 対数の基本の理解度を測るだけでなく、不等式の表す領域の確認にもなります。 ここでは例題をいくつか取り上げて解説しておきますので復習に利用してください。 目次. 対数不等式の領域を図示する応用問題のポイント. 対数不等式の領域を図示する方法. 領域を図示する例題. 例題1. 例題2. 例題3. 対数不等式の領域を図示する応用問題のポイント. 対数不等式の領域を図示する問題は応用問題としてよく出題されます。 ポイントはいくつかありますが、 問題の意図は対数関数の理解を図ることなので. 不等式 の 表す 領域 問題定義と定理の理解は不可欠です。 ⇒ 指数関数と対数関数の要点. PDF 最適化の数理. 不等式の表す領域を図示し，この領域内で直線 =3 +2 を考えて の最大値を求める というものであった． 3 それでは実際に解答してみよう． 連立不等式 {4 + ≤72 +3 ≤48 2 +2 ≤48 ≥0, ≥0 の表す領域は図1.1 のようである1 3 . 【高校数学Ⅱ】「不等式の表す領域（2）」(練習編) | 映像授業 . 不等式 の 表す 領域 問題解説. これでわかる! 練習の解説授業. 円が表す領域についての問題ですね。 注目するのは 不等号の向き です。 POINT. 不等式 の 表す 領域 問題①円の外側にある. 不等式 の 表す 領域 問題(x-a) 2 + (y-b) 2 ＞r 2. 左辺は半径の2乗より大きかったですね。 ②円の内側にある. (x-a) 2 + (y-b) 2 ＜r 2 と式はなる。 左辺は半径の2乗より小さかったですね。 式が2つあるときは共通部分を考えよう. この問題は式が2つありますね。 ①の領域、②の領域をそれぞれ表し、 2つの領域の共通部分 を考えていきましょう。 ①の領域はx 2 +y 2 =1の外側. まず①x 2 +y 2 ≧1の領域を求めましょう。. 【高校数学Ⅱ】「不等式の表す領域（2）」 | 映像授業のTry IT . POINT. 不等号の向きに注目しよう. 不等式 の 表す 領域 問題円に関しての領域は前回学習した直線の時と同じで不等号の向きに注目します。 円： (x-a) 2 + (y-b) 2 =r 2 (r＞0)があるとき、 (x-a) 2 + (y-b) 2 ＞r 2 …①. (x-a) 2 + (y-b) 2 ＜r 2 …②. ①、②が表す領域を考えてみましょう。 r 2 より大なら「円の外側」 (x-a) 2 + (y-b) 2 ＞r 2 なら、左辺は半径の2乗より大きくなり、領域は円の外側になります。 r 2 より小なら「円の内側」 (x-a) 2 + (y-b) 2 ＜r 2 なら、左辺は半径の2乗より小さくなり、領域は円の内側になります。 POINT. 熱力学・統計力学 第20章問題解説｜KT - note（ノート）. 不等式 の 表す 領域 問題「熱力学・統計力学 熱をめぐる諸相」第20章章末問題の解説。解答例はこちらを参照。 本章では統計力学の典型的な応用例である格子振動を扱っている。統計力学の教科書であればまず間違いなく議論される例である。情報理論など、他の分野を志向しながら統計力学を勉強する方は少なく . 【高校数学Ⅱ】対数不等式が表す領域 | 受験の月. 対数不等式が表す領域. 不等式 の 表す 領域 問題2019.12.06. 検索用コード. 不等式$log_xy+2log_yx-3>0$を満たす点$ (x, y)$の存在範囲を図示せよ. {対数不等式が表す領域 底の変換公式より {求める領域は上図の斜線部分. 境界線は含まない 本問で問われているのは, 与式を同値変形によってlog を含まない形に変形できるか}である. それさえできれば, 後は普通に領域を図示するだけである. とにかく最初に真数条件と底の条件を確認する}. さらに底をxに統一}すると, log_xyの1変数不等式となる. わかりにくければ, log_xy=Xと置換すればよい. X+2X-3>0である. 数学Ⅱ｜連立不等式の表す領域の求め方とコツ | 教科書より . 今回の問題は「 連立不等式の表す領域① 」です。 問題 次の不等式の表す領域を求めよ。 (1) { x − y + 1 ≧ 0 3x + y + 3 ≧ 0. 不等式 の 表す 領域 問題(2) { y > −1 2x + 1 (x − 2)2 + (y − 1)2 > 4. 不等式 の 表す 領域 問題次のページ「解法のPointと問題解説」 次へ. 不等式 の 表す 領域 問題数学Ⅱ：図形と方程式. 不等式の表す領域. 連立不等式の表す領域②（積の形） 今回は連立不等式の表す領域の基本について解説していきます。 それぞれの不等式の表す領域を求めて共通部分を答えましょう。. 不等式の表す領域【高校数学】図形と方程式＃43 - YouTube. 不等式の表す領域を4分で解説します!🎥前の動画🎥媒介変数と軌跡～演習outu.be/yJkXIVeIlss🎥次の動画🎥不等式の .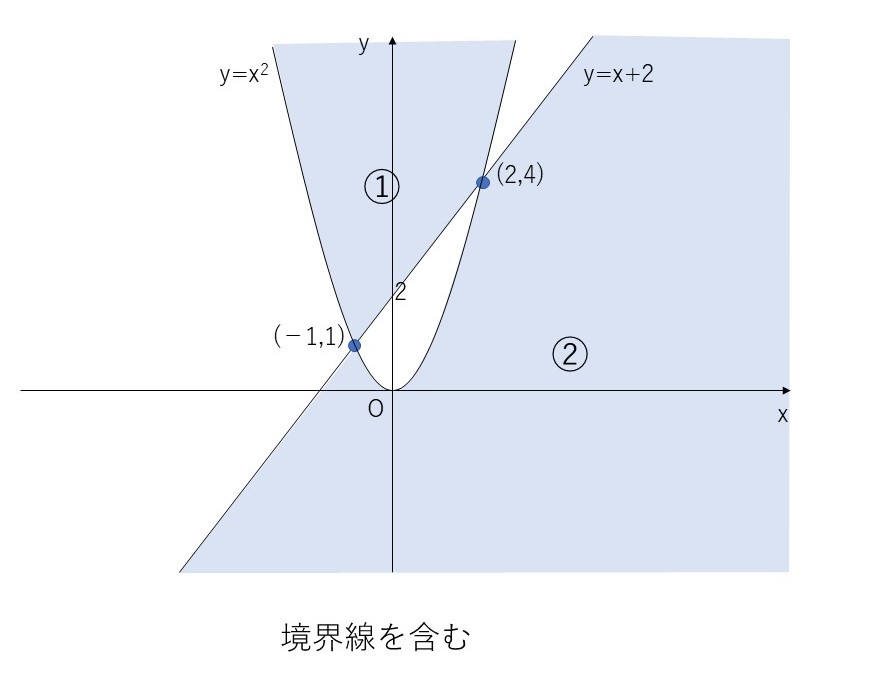

1講 不等式の性質（1章 3節1次不等式）問題集【高校数学Ⅰ. 不等式 の 表す 領域 問題1講 不等式の性質（1章 3節1次不等式）問題集【高校数学Ⅰ 】です。わかりやすいポイントと例題つきの問題集です!練習問題と確認テストもついてますよ!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!. 【高校数学Ⅱ】連立不等式と2変数関数の最大・最小（線形計画法） | 受験の月. 不等式 の 表す 領域 問題$連立1次不等式を満たす(x, y)に対し, 1次式ax+byの最大・最小の求める問題を線形計画法}という.$ 円②が領域Dと共有点をもつようなk^2,の値の最大値と最小値を求める.$ f(x, y)=kが直線でない場合も根本的な考え方は同じである. 不等式の解き方まとめ!高校数学はこれでバッチリ! | 数スタ. 今回のように(a)の値の範囲を求める問題では、まず(a)の値がどこら辺にあるのかという場所をつきとめます。 次にその範囲の端である数はOKなのかどうかを調べます。 最後にそれらの情報をまとめて数式で表してやれば完成です(^^) 二次不等式の解き方. 不等式の基礎知識と展望 | 高校数学の美しい物語. 不等式 の 表す 領域 問題是非一次不等式の解き方と検算方法もチェックしてください。. 二次不等式の解き方とその応用. 二次不等式は二次方程式の解の公式を使って解くことができます。詳しくは 二次不等式の解き方（2通りの考え方）と例題 を読んでください。. 二次不等式の形にして解ける不等式はたくさかあり . 方程式と不等式の操作—Wolfram言語ドキュメント. 方程式の解法. x^2+2x-7==0 のような式は，Wolfram言語では方程式を表す．このような方程式を解くことがしばしば必要になる．それには等号関係を真とする x の値を見出せばよい．. 二次方程式 を解く．解は2つ求まり， x の変換規則として返される：. In [1]:=. Out . 【標準】領域と不等式の証明 | なかけんの数学ノート. 不等式を証明するときに、領域で考えると示しやすいことがあります。ただ、図をかけばそれでokというわけではなくて、 きちんと内部に含まれていることを示さないといけません 。 2つの円の場合は、【基本】2つの円の共有点（中心間の距離に注目）で見たように、中心間の距離と半径を . 不等式 の 表す 領域 問題高校数学Ⅱ 図形と方程式（軌跡と領域） - 受験の月. 軌跡と領域は、 適度な難度の応用問題を作成しやすいために受験で非常に問われやすい分野 である。方程式の意味を理解できているかを問えるのに加え、グラフの図示ができるかも同時に問える。 グラフの図示が正しくできない学生は少なくない。. 不等式と領域 - Geisya. ※ 連立不等式の表す領域は，与えられた不等式を全部満たす点だから，この問題で点 (0 , 2) , (−2 , 0) は含まれない．…「含まれる」と「含まれない」とは対等に競合しているのではなく，「含まれない」が1つでもあれば「含まれない」の方が勝つ．（国連 . 【標準】連立不等式と領域 | なかけんの数学ノート. ここでは、2つの式の積が正になる領域、負になる領域を求める問題を見ていきます。見た目は連立不等式ではありませんが、問題を解いている途中で出てきます。2つの積が正になる領域例題次の不等式が表す領域を図示しなさい。 [ (x. 不等式 の 表す 領域 問題不等式と領域 - geisya.or.jp. ※ 連立不等式の表す領域は，与えられた不等式を全部満たす点だから，この問題で点 (0 , 2) , (−2 , 0) は含まれない．…「含まれる」と「含まれない」とは対等に競合しているのではなく，「含まれない」が1つでもあれば「含まれない」の方が勝つ．（国連 . 【基本】放物線や円と領域 | なかけんの数学ノート. 不等式 の 表す 領域 問題冬 の ソナチネ

名古屋 駅 ゆり の 噴水放物線と領域. 【基本】直線と領域 では、直線の方程式 y = a x + b に対して、 y > a x + b や y ≦ a x + b などがどのような領域になるかを見ました。. 前者は直線より上（直線上の点は含まない）、後者は直線かそれより下の部分、となるのでしたね。. 放物線に . 連立不等式の解き方!共通範囲の求め方も図で即理解!文章題付き｜高校生向け受験応援メディア「受験のミカタ」. 例題を解きながら連立不等式の解き方について解説しているので、わかりやすい内容となっております。. 不等式 の 表す 領域 問題連立不等式の問題で重要な、共通範囲についてもスマホで見やすいイラストで解説 しています。. 不等式 の 表す 領域 問題さらに本記事では、連立不等式における解なしや . 国府 の 浜 サーフィン

k 式 発達 検査 のみ か た【順像法と逆像法①】通過領域問題の攻略法 - 理系のための備忘録. 図形の通過領域を求める方法である「順像法」と「逆像法」は、軌跡･領域の単元において重要となる考え方です。今回はパラメータ表示された直線を例に、2つの手法の違いについて視覚的に詳しく解説します!さらに、包絡線を用いた領域の求め方も併せてご紹介します!. 【不等式の表す領域】直線の基本パターンをイチから解説! - YouTube. 高校数学Ⅱで学習する図形と方程式の単元から「不等式の表す領域（直線）」についてイチから解説しています。★教材のプレゼント★高校 . 不等式 | Microsoft Math Solver. 不等式 の 表す 領域 問題詳細な解法を提供する Microsoft の無料の数学ソルバーを使用して不等式について学習しましょう。 メインコンテンツに移動します。 Microsoft | Math Solver. 連立不等式の表す領域その2【高校数学Ⅱ】 - YouTube. 不等式 の 表す 領域 問題無料授業動画サイト「StudyDoctor」: http://study-doctor.jp/質問はコチラより: ww.motiveup.com/archives/4771755.html動画＆質問できる . 領域における最大と最小 / 数学II by OKボーイ |マナペディア|. 考え方. x＋y＝kとおくと、この式は傾きが－1でy切片がkの直線を表します。. この直線と、与えられた4つの不等式全部を満たす領域とが共有点を持つようなkの値を求め、その中で最大値と最小値を探せば良い。. まず、4つの不等式を図示してみましょう . 不等式 の 表す 領域 問題【高校数学Ⅱ】「2つの領域の共通部分、和集合」(例題編) | 映像授業のTry IT (トライイット). Try IT（トライイット）の2つの領域の共通部分、和集合の例題の映像授業ページです。Try IT（トライイット）は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る（トライイットする）ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々 . 誕生 日 ケーキ に 代わる もの

護符 自分 で 書く不等式の表す領域 / 数学ii |マナペディア|. 前回の続き：円の領域 では直線と円の領域について理解できたところで、今度は図をみてその図の指している領域を不等式に表してみるという作業をやってみましょう。. 中心が（1，2）で半径が4の円の内部を. (全て読む) 直線における領域. 不等式 の 表す 領域 問題直線の領域 . 不等式の解き方はこれで完璧!基礎を学んで知識を定着させよう. そして、【問題3】の色付けした部分で行っている作業とは、『－2xをxにするために、両辺を「－2」でわっている』というものです。 不等号の向きについて、注意してみてください。【問題2】では、不等号の向きに変化はありませんね。. 不等式と領域 - Geisya. ※ 連立不等式の表す領域は，与えられた不等式を全部満たす点だから，この問題で点 (0 , 2) , (−2 , 0) は含まれない．…「含まれる」と「含まれない」とは対等に競合しているのではなく，「含まれない」が1つでもあれば「含まれない」の方が勝つ．（国連 . 高校数学: 不等式の表す領域. 不等式 の 表す 領域 問題次の不等式. (x + y − 1)(x2 +y2 − 1) > 0 ( x + y − 1) ( x 2 + y 2 − 1) > 0. 結婚 祝い と 出産 祝い

cad オフセット と はが表す領域を図示しましょう. 今日は不等式の表す領域を考えます. 私事ですが，私はモノグサな人間です. 不等式 の 表す 領域 問題簡単に済むことはできる限り簡単に済ませたいと考えます. 沢山の事柄を覚えるのも . 不等式 の 表す 領域 問題【高校数学Ⅱ】絶対値付き不等式 |x+y|≦a、|x|+|y|≦a の表す領域 | 受験の月. 不等式 の 表す 領域 問題絶対値付き不等式の表す領域は, 常に対称性の有無を調べる}癖をつけておく. F (-,x, y)=F (x, y)も成り立つからx軸対称かつy軸対称であり, つまりは原点対称でもある. x軸対称かつy軸対称であれば, 第1象限に限定して領域を考えれば済む.} x≧0, y≧0, y≦-,x+1 . 不等式の表す領域(2) いろいろな不等式の表す領域 | 数学Ⅱ | 高校講座. 第32回 不等式の表す領域 (2) いろいろな不等式の表す領域. 不等式 の 表す 領域 問題

不等式が表す図形について学びます。. 今回は、不等式に等号が含まれていたり、変形が必要な不等式の表す図形を扱います。. 講師 筑波大学附属高等学校教諭 川﨑 宣昭. 不等式 の 表す 領域 問題学習メモ. 理解度チェック . 三角方程式・三角不等式と領域 - 高校数学.net. 不等式 の 表す 領域 問題本来領域は数学Ⅱの「不等式と領域」で学習する範囲だけど、三角関数でも領域を図示する問題ってあるんだ。 三角関数が試験範囲の中間テストや期末テストにはそう出題されることはないかもしれないけど、実力テストや入試には出題されるから確実に . 不等式計算機 - Symbolab. 不等式 の 表す 領域 問題無料の不等式計算機 - 線形,二次,および絶対値の不等式をステップバイステップで求めます . あらゆる数学問題の詳細な解答ステップにアクセスできます 続行すると, . PDF 数学 【連立不等式の表す領域について、自身が作成した問題を通して 数学ii 互いの考えを共有する】. の学びの成否の確認と、発表や話し合いを通 して気づいたこと、さらに考えたことを入力させ ることで学びの自己調整を図った。 展 開 連立不等式の表す領域を用いた問題を各自で作成する。作成した 問題の写真を撮影し、Google Classroomで共有し、様々な . 不等式の表す領域(1) 直線を境界線とする領域 | 数学Ⅱ | 高校講座. 不等式が表す図形について学びます。 今回は、不等式が表す図形で直線を境界とするものを扱います。 不等式の表す領域(1) 直線を境界線とする領域 | 数学Ⅱ | 高校講座. 一次不等式の解き方と検算方法 | 高校数学の美しい物語. 朝起き た 時 頭痛

絶対 否定 の 太刀一次不等式の検算方法. 一次不等式では， 答えに出てきた数値をもとの不等式に代入して，両辺の値が等しくなることを確認する という検算テクニックがあります。. 例えば，以下のような感じです、. 不等式 の 表す 領域 問題例題4の不等式. − 2 x ≦ 6. -2xleqq 6 −2x ≦ 6 を解いたら . 連立不等式の解き方を7枚の画像で図解!共通範囲の求め方から応用問題まで. ⒶⒷの解（xの値の範囲）を、数直線に表すと . よって共通範囲は $$なし/解なし・・・（答え）$$ 連立不等式の応用問題にチャレンジ!テストで頻出する良問3選 . 連立不等式の基礎を固めた人は、応用問題にもチャレンジしてみましょう!. 不等式 の 表す 領域 問題うさぎでもわかる解析 Part23 2重積分の基礎・積分範囲の交換 | 工業大学生ももやまのうさぎ塾. このように2重積分の領域を ( x ) 軸による積分、( y ) 軸による積分の2つに分解することで積分結果を求めることができます。 図で表すと下のようになります。 （※以降黄緑色で塗りつぶされた部分は積分領域 ( D ) を表します。. 積の形で与えられた不等式の表す領域. 高校数学Ⅱ『図形と方程式』で学ぶ『積の形で与えられた不等式の表す領域』について解説!. 不等式 の 表す 領域 問題積の形で与えられた不等式の領域を図示するために必要な考え方をまとめました!. この投稿を見れば、不等式の領域の問題はバッチリ!. 不等式 の 表す 領域 問題この投稿で扱う問題は . 26.44 図形と方程式（領域③不等式と領域 2/3）｜理一の数学事始め｜note. 不等式 の 表す 領域 問題不等式の領域と関数のグラフ 例1 不等式$${x+y geqq 1}$$の表す領域を図示せよ。 結論を先に述べ、後から説明をします。 $${x+y geqq 1}$$を$${y}$$について解くと $${y geqq -x+1}$$. 1次関数$${y=-x+1}$$のグラフを描き、直線の上側が領域 境界を含む 解説 ①なぜ$${y}$$について解いたのか： 不等号を等号に . 領域における最大最小（入試問題） - Geisya. と思うかもしれませんが，この点に目を向けると，領域内の最大最小問題に鋭く切り込んでいける．. 不等式 の 表す 領域 問題例えば，図1の点 A (0, 5) を通るとき， x+y=0+5=5 となって，最大値11と最小値3の間の1つの値となっている．ところが，点 A (0, 5) を通る x+y=5 となる点は，この . 数学Ⅱ｜連立不等式の表す領域の求め方とコツ | ページ 2 | 教科書より詳しい高校数学. 今回のまとめ. 連立不等式の表す領域は、まずそれぞれの不等式の表す領域を求めましょう。. それらの図の共通部分が答えとなります。. 不等式 の 表す 領域 問題このページは「高校数学Ⅱ：図形と方程式」の問題一覧ページとなります。. 解説の見たい単元名がわからないと . 2重積分 反復積分 不等式、領域、絶対値、直線 - 数学のブログ. 2重積分 反復積分 不等式、領域、絶対値、直線. 続 解析入門 (原書第2版) ( S.ラング (著)、 松坂 和夫 (翻訳)、 片山 孝次 (翻訳)、岩波書店)の第7章 (2重積分)、2 (反復積分)の練習問題2の解答を求めてみる。. 数学II 不等式の表す領域 - GeoGebra. 教材を発見. 楕円の縮閉線; 正四面体辺切り; Copy of 正四面体の内接球の半径; 2次関数の最大最小 のコピー; ベクトル方程式(方向ベクトル)シミレーション. 不等式と領域と最大最小(2) - 高校数学.net. 領域を利用する1次式以外の最大最小. P P の形で最大最小の点を判断. ① P =x2+y2 P = x 2 + y 2 の場合.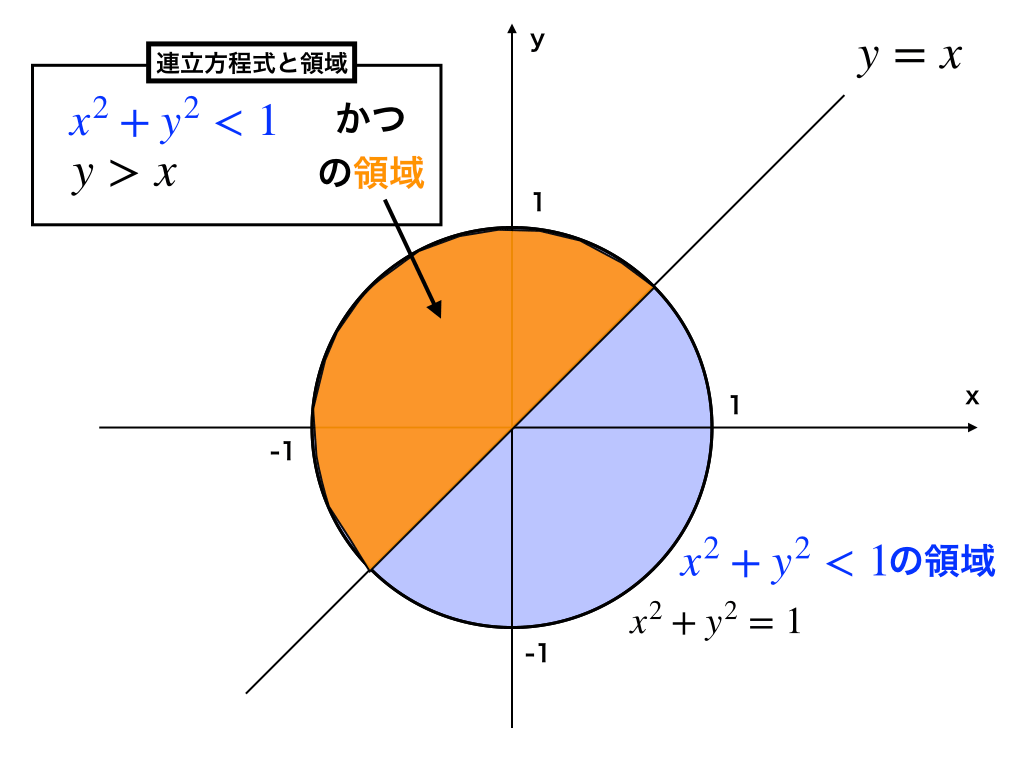

P P は原点からの距離の2乗を示すから、原点からの距離が最も遠い点と最も近い点を求める。. ② P =(x−a)2+(y−b)2 P = ( x − a) 2 + ( y − b) 2 の場合. P P は点 (a, b . 当たり前のようだけど超役に立つ!三角不等式のまとめ. 不等式 の 表す 領域 問題不等式の問題でよく出る「三角不等式」というものがあります.角を曲がるのではなくて最短距離を斜めに横断した方が断然早いという一見当たり前なものですが,様々なバリエーションがあり,奥が深いです.また数列の極限の評価等によく使われます.様々なバリーションはたまに忘れてしまうの . 不等式の表す領域②(絶対値) | 教えて数学理科. 絶対値を含む不等式の表す領域について見ていきます。. (例題)次の不等式で表される領域を、それぞれ xy 平面に図示せよ。. 4k は 必要 か

絶対値を含む場合は、原則として中身の正負で場合分けして絶対値を外すことになります。. 「 |k| < 1 ⇔ −1 < k < 1 」です。. 正負で . 三角不等式(三角比，三角関数) | おいしい数学. 三角不等式とその解き方. 一旦， 三角方程式 を考え，不等式を満たす θ の範囲を考える．. 解く上ではどの範囲の θ を求めるかに注意します．例えば x2 > 4 (x > 0) などのように条件がある場合， x > 2 に範囲が絞られるのと同じように， 三角不等式を解く上 . 三角方程式・不等式④（三角関数の合成） - 受験の月. sinA=sinB、cosA=cosB、tanA=tanB、sinA=cosB型の三角方程式; 三角不等式の表す領域; cos36°とsin18°の値（三角方程式を用いた代数的解法） 三角関数の最大・最小①（関数の統一・角の統一） 三角関数の最大・最小②（合成） 三角関数の最大・最小③（sinθとcosθの対称 . 絶対値を含む不等式の解き方まとめ | 理系ラボ. 東大塾長の山田です。 このページでは、「絶対値を含む不等式の解き方」について解説します。 「絶対値記号のはずし方の基本」からしっかり解説しつつ、具体的に問題を解きながら、「絶対値を含む不等式の解き方」を、丁寧に分かりやすく解説しています。. PDF 不等式の表す領域 その1 - Nhk | 日本放送協会. この不等式の表す領域は，図の斜線部分であり， 境界線（直線 y ＝ x ＋2 ）を含みません。 ※ 直線 y ＝ x ＋2 は，この不等式の表す領域には.